#机器学习13--EM算法--应用到三个模型： 1,2,3因子分析模型 使用场所： > - 标签z是连续的 - 样本个数大于特征数 - 高维-->低维 - 潜在的假想变量和随机影响变量的线性组合表示原始变量
##边缘和条件概率分布 后面的推导用到了边缘和条件分布： 1. 已知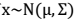 
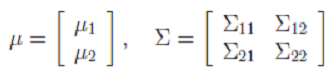2. 边缘分布 
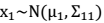3. 条件概率分布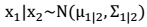 
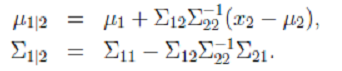
###因子分析模型 z被称为因子。我们要做的就是从高维随机连续变量x，变换到低维随机连续变量z。 1. 首先，我们如下假设： 
> eg：从1维到2维： 1维： 
2维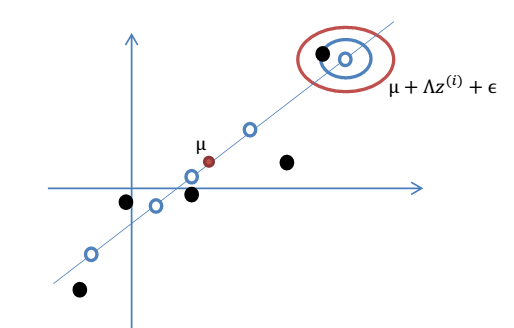 
2. 我们令：
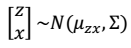3. 下面经过推导，求得
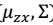的具体值：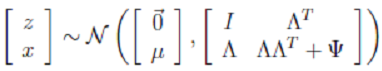 
4. 因此，我们得到x的边缘分布： 
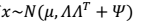5. 从而我们对样本 
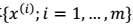进行最大似然估计：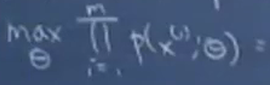 
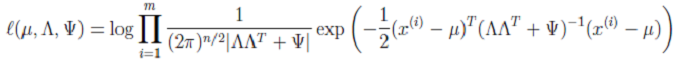> 但是，当似然函数最大时，我们得不到解析解（比如，一元二次方程的通解形式）。根据之前对参数估计的理解，在有隐含变量 z 时，我们可以考虑使用 EM 来进行估计。
###因子分析的EM估计 ####总体步骤： 
> 注：这里的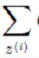
要改写为积分符号\(\int_{z^{(i)}}^{}\)。因为，z是连续随机变量。
####详细步骤 E步 1.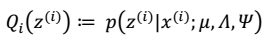 
根据前面的结论有：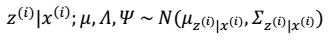 
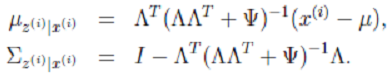2. 根据多元高斯公式得：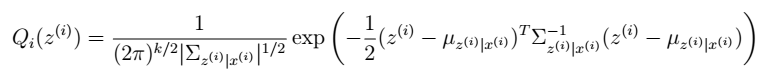 
M步 3. 我们目标是最大化：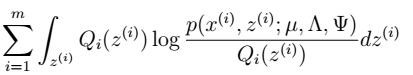 
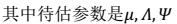4. 通过参数估计，我们最终可以得到：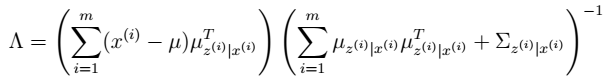 
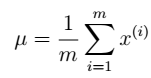
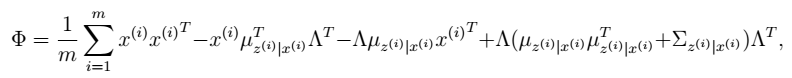然后将Φ上的对角线上元素抽取出来放到对应的Ψ中，就得到了Ψ。
###因子分析总结 1. 根据上面的 EM 的过程，要对样本 X 进行因子分析，只需知道要分解的因子数（z 的维度）即可。通过 EM，我们能够得到转换矩阵Λ和误差协方差Ψ。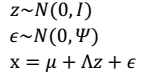 
2. 因子分析(factor analysis)是一种数据简化的技术。原始的变量是可观测的显在变量，而假想变量是不可观测的潜在变量，称为因子。 3. 因子分析与回归分析不同，因子分析中的因子是一个比较抽象的概念，而回归因子有非常明确的实际意义 4. 主成分分析分析与因子分析也有不同，主成分分析仅仅是变量变换，而因子分析需要构造因子模型。 > 主成分分析:原始变量的线性组合表示新的综合变量，即主成分； 因子分析：潜在的假想变量和随机影响变量的线性组合表示原始变量。
