机器学习8--支持向量机（下）
上节回顾：从逻辑回归引出支持向量机-->定义函数间隔和几何间隔-->最优间隔分类器（通过最大化间隔，得到最优）-->引出拉格朗日对偶（作用：通过对偶将算法变得更高效；处理高维）-->将对偶用到最优间隔分类器 本节内容：核函数（升维）-->判定是否是有效的核函数-->L1 norm 软间隔SVM（针对不可分的情况）-->第三种求解最优化的方法：坐标上升法-->SMO优化算法（最快的二次规划优化算法）
核函数
1、定义 >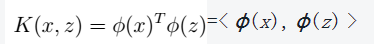 
2、核函数的作用 > a、低维映射到高维，从而更好的拟合； b、将不可分的情况变为可分
3、举例： > 例一：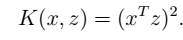 
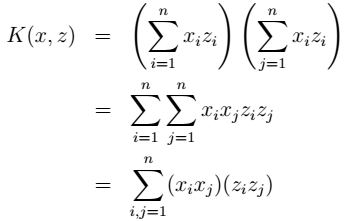说明：时间复杂度由
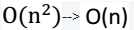例二： 高斯核（把原始特征映射到无穷维）：
映射后的优点： 
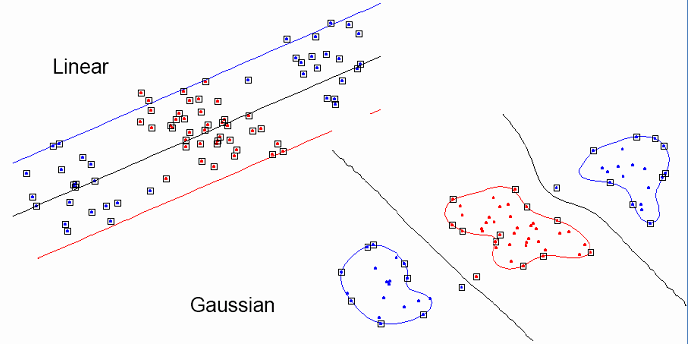
4、映射后怎样进行预测： > 预测函数：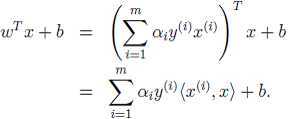
映射后：将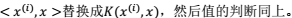
问题：怎样求取和判断核函数？下面将会介绍。
核函数的判定
1、符号说明 > K：核函数矩阵$K={K_{ij}} $ 第i,j个样本 \(K_{ij}\) 或者$K(x{(i)},x{(j)}) $ ：核函数$K_{ij}=K(x{(i)},x{(j)}) $
2、利用Mercer定理 > 
简而言之，K是一个有效的核函数<-->核函数矩阵是对称半正定
L1 norm 软间隔SVM
当不可分时，利用L1 软间隔进行分离 1、 加入软间隔后的模型： > （1）凸规划：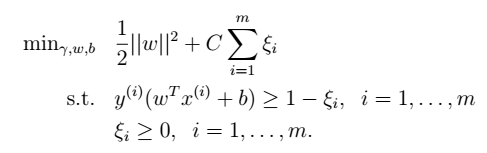 
其中，C是离群点的权重（我们预定的，为已知数），越大表明对目标函数影响越大，也就是月不希望看到离群点。引入非负参数
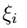（称为松弛变量） ， 就允许某些样本点的函数间隔小于1，即在最大间隔区间里面，或者函数间隔是负数，即样本点在对方的区域中。 （2）拉格朗日算子： 
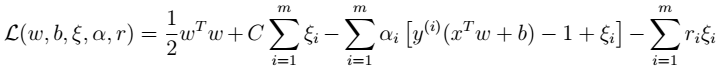其中，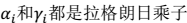
（3）推导结果 跟前面模型类似：先写出拉格朗日公式 （如上） ，然后将其看作是变量 w 和 b的函数，分别对其求偏导，得到 w 和 b 的表达式。然后代入公式中，求带入后公式的极大值。得到： 
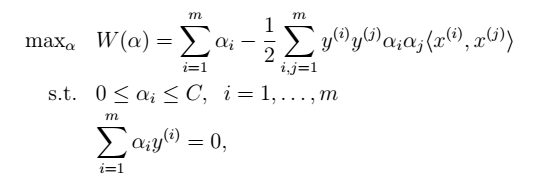>> KTT条件：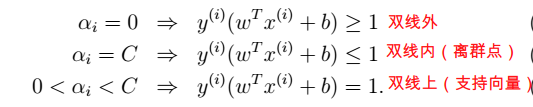 
第三种求解最优化的方法：坐标上升法
1、三种求解最优化的方法： > （1）梯度上升法(求解最小值问题时，称作梯度下降法) （2）牛顿法（求解最值） （3）坐标上升法（求解最小值问题时，称作坐标下降法）
2、假设求解下面问题： >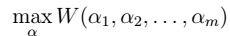 
其中，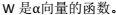
3、算法过程： >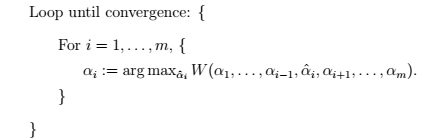 
>> 
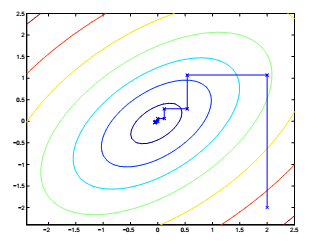
SMO优化算法
最快的二次规划优化算法，特别针对线性 SVM 和数据稀疏时性能更优。 1、前面得到的结果 > 首先，先看前面的到的结果，如下图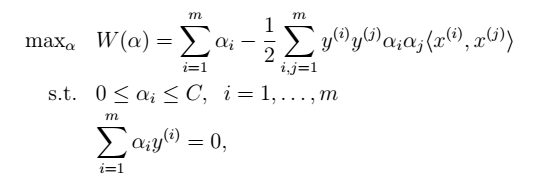： >> 这个问题中： 
按照坐标上升法的思路，只固定一个
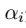的话，由于限制条件中存在
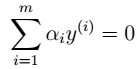，将导致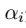不再是变量。 因此，我们一次选取两个参数做优化。
2、SMO的主要步骤 > 
注：第一步，利用启发式方法选取
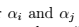。第二步，固定其他参数，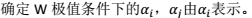
3、 具体步骤 > （1）固定除
以外的参数，得：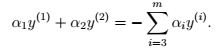 
（2）为了方便: 
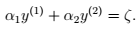>> 如下图： 
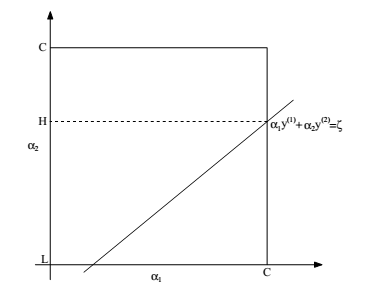其中，满足：
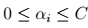和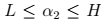
L和H的范围： 
（3）将
带入W中：
展开，得：
（4）这就是二次函数的最小值问题，容易求得（在纸上画图很容易看出来）：
其中，
为最终结果。
为求导得到的结果。 同理，求得
的最优解。
总结
1、本章的系统结构： > 至此，我们得到： 预测问题只需要求解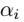
，即： 
<-->上面的过程（SMO）求得
为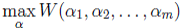
的最优解 <-->
<-->
<-->
<-->
<-->
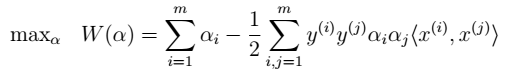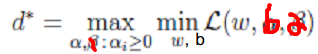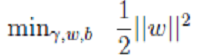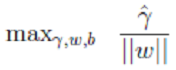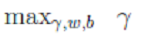（最大化几何间隔问题）
2、关于核问题（升维）的说明 > 核问题用来替换第一步中的部分：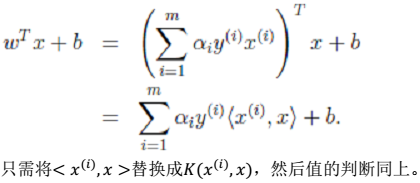 
### 形式化表示LR-->SVM表示 
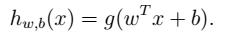
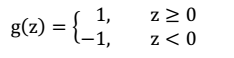
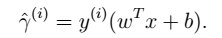所有训练样本：
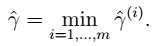- 几何间隔 一个训练样本：
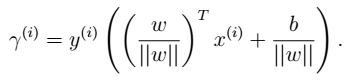所有训练样本：
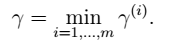- 两者关系 当
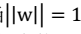时，两者等价。
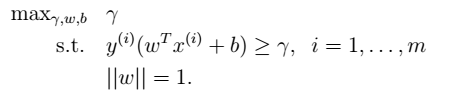- 函数间隔的优化 
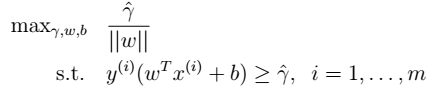- 改写后的规划：令
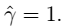，这样做的意义：将全局的函数间隔定义为1，即将离超平面最近的点的距离定义为
，
： 
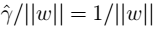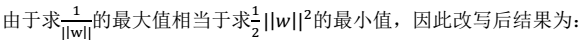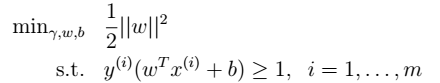
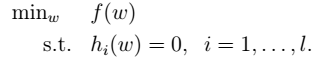
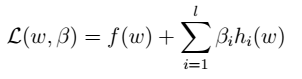其中，l为约束的个数（样本数目），
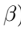为拉格朗日乘数。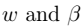
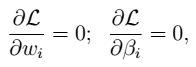
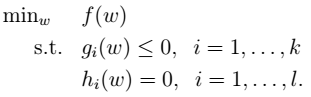
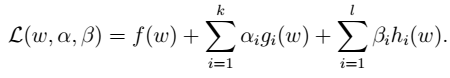其中，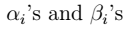
为拉格朗日乘数。
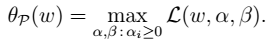即： 
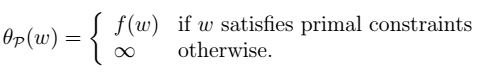
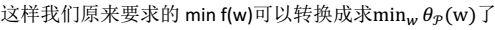
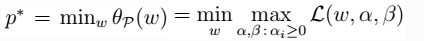
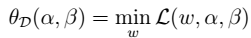，则：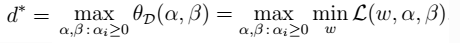 
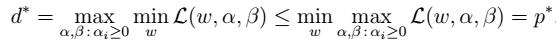
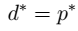的条件，KKT条件： 
，即KKT条件：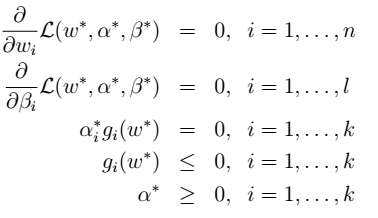 
> 注: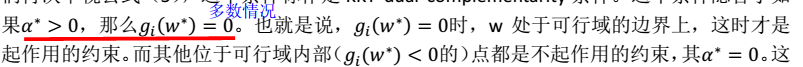
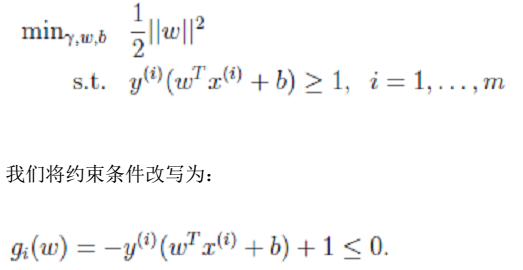
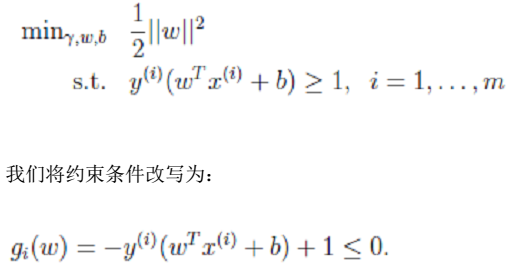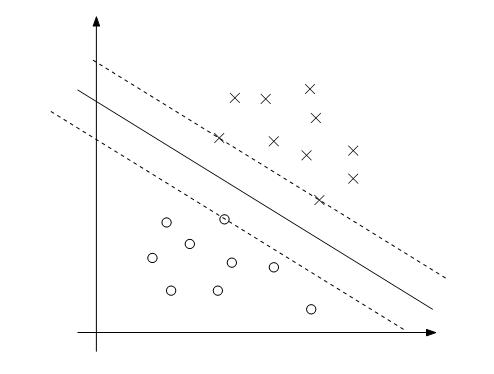
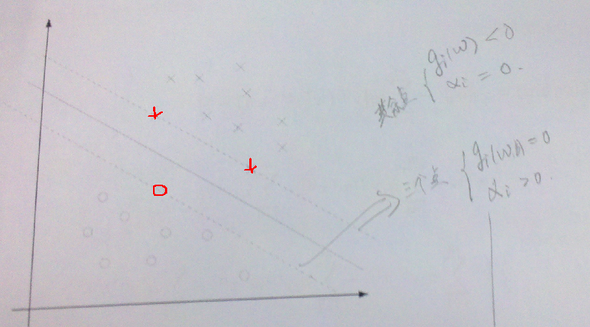
- 2、拉格朗日算子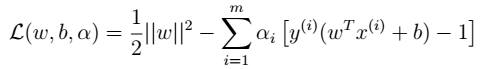 
- 3、没有等式约束，只有不等式。下图中虚线上的三个点称为支持向量（支持向量机中的支持向量）。三点的函数间隔为1。
。 
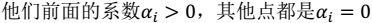### 求解最优化问题 - 1、对偶问题 
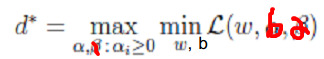- 2、求解极小化问题：对w求偏导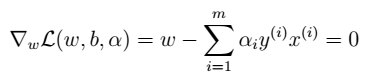 
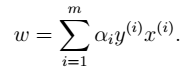- 3、求解极小化问题：对w求偏导 
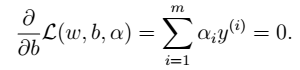- 4、将w，b带入L中 
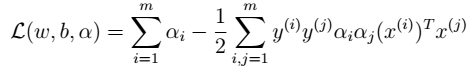注：该函数是关于
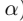的函数。通过极大化，来求解得到该值。然后，再得到w和b。 - 5、求解极大化问题：
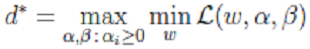凸规划：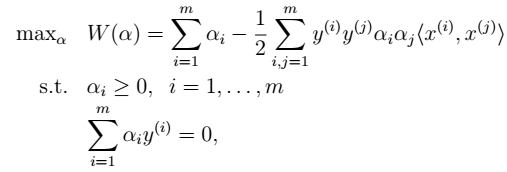 
- 6、求解 > 求解得到
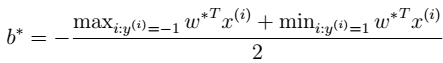得到b。 其中，b的意义：离超平面最近的正的函数间隔要等于离超平面最近的负的函数间隔。 - 7、进行预测 如下公式所示:有了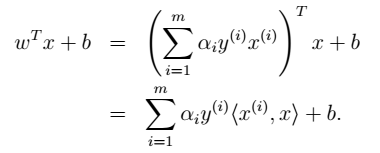
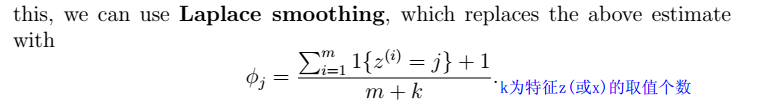平滑后的NB参数：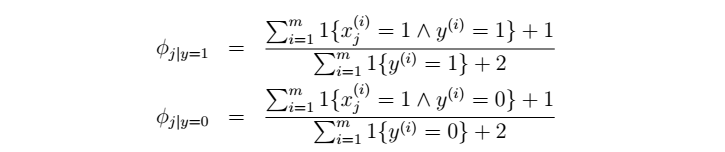 
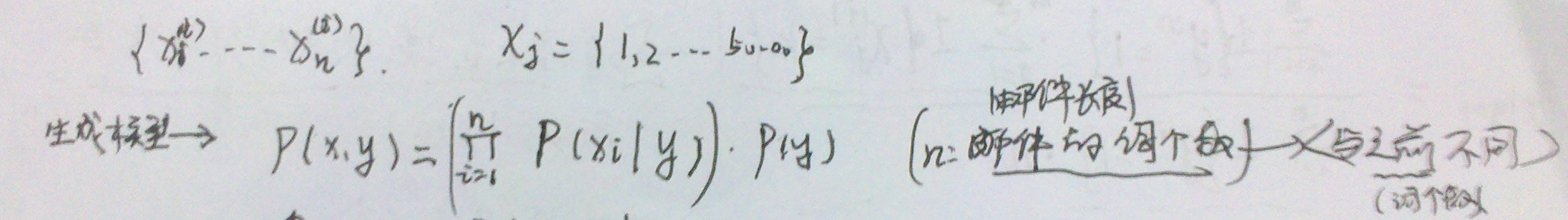
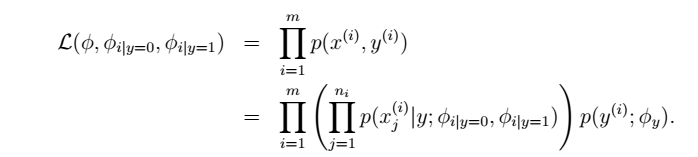
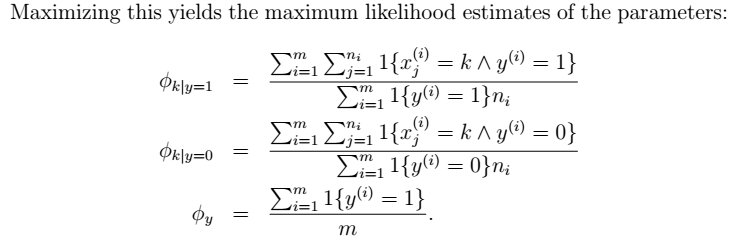
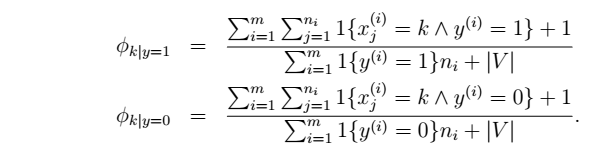
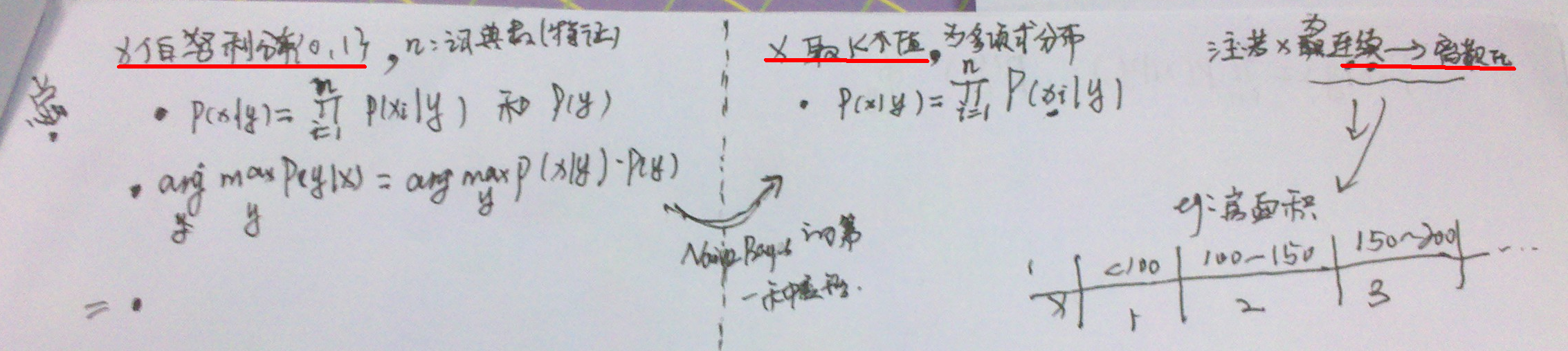
得到梯度下降的基本算法，下面会对其展开详细说明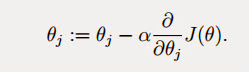 
###1.1 批量梯度下降 缺点：不适合数据量很大的情况 
###1.2 随机梯度下降 
###1.3 另外一种最小化
##3.逻辑回归（第一种：最大化
