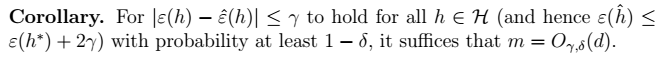#机器学习12-1--K-means算法(无监督) 本章开始接触第一个无监督学习算法。无监督学习算法可用在新闻局累、图像分割等。 ## 无监督学习概念 - 定义:简单讲,就是没有分类标签y。非监督式学习是一种机器学习的方式,并不需要人力来输入标签。它是监督式学习和强化学习等策略之外的一种选择。 - K-means是最简单的聚类,聚类属于无监督学习。
K-means的步骤
- 符号: > 类的数目:\(k\) 训练样本:
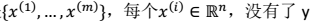 质心点:
质心点: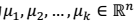 类:\({c^{(1)}, c^{(2)}, ……, c^{(k)}}\)
类:\({c^{(1)}, c^{(2)}, ……, c^{(k)}}\) - 步骤: K-means 算法是将样本聚类成 k 个簇(cluster),具体算法描述如下:

- 二维效果图(k=2):
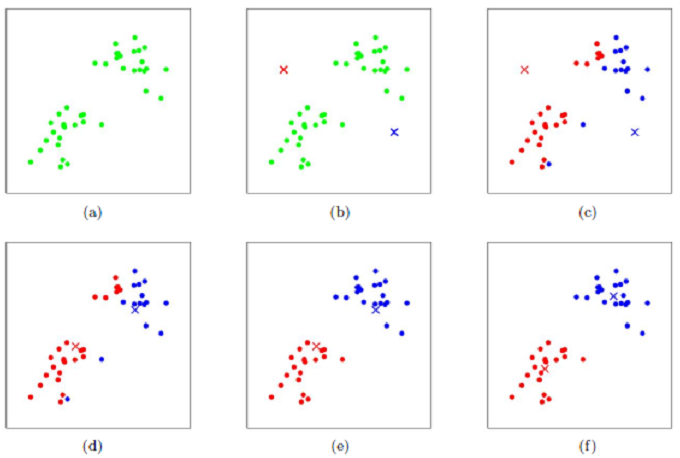
- Kmeans收敛的原因 > 首先,我们定义畸变函数(distortion function)如下:
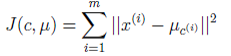
 注:由于畸变函数 J 是非凸函数,意味着我们不能保证取得的最小值是全局最小值,也就是说 k-means对质心初始位置的选取比较感冒,但一般情况下k-means达到的局部最优已经满足需求。但如果你怕陷入局部最优,那么可以选取不同的初始值跑多遍 k-means,然后取其中最小的 J 对应的μ和 c 输出。
注:由于畸变函数 J 是非凸函数,意味着我们不能保证取得的最小值是全局最小值,也就是说 k-means对质心初始位置的选取比较感冒,但一般情况下k-means达到的局部最优已经满足需求。但如果你怕陷入局部最优,那么可以选取不同的初始值跑多遍 k-means,然后取其中最小的 J 对应的μ和 c 输出。 - 聚类后结果是一个个星团,星团里面的点相互距离比较近,星团间的星星距离就比较远了。
K-means与EM的关系:
EM的基本思想: > - E步:固定参数θ,优化隐含类别Q > - M步:固定隐含类别Q,优化参数θ
K-means用到的EM的基本思想: > - E步:确定隐含类别变量c > - M步:更新其他参数μ来使J最小化
两种算法都类似于坐标上升法。固定一个,优化另外一个。
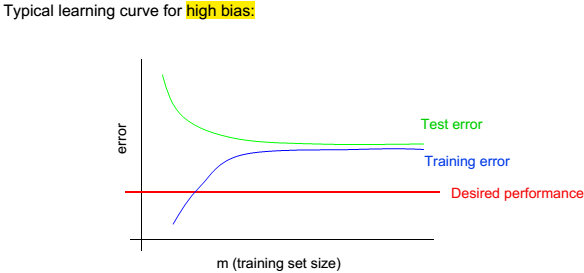
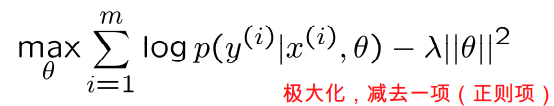 2、如果,误差太大,我们怎样做?
2、如果,误差太大,我们怎样做?  3、很显然,这样很耗时。
3、很显然,这样很耗时。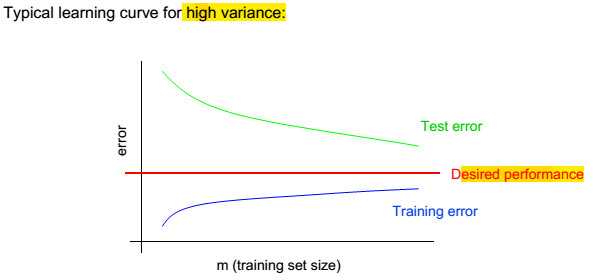





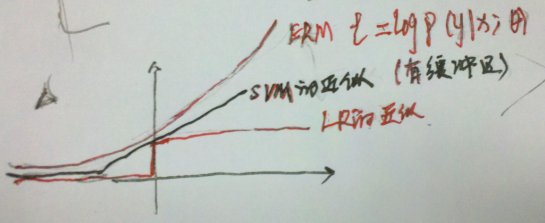
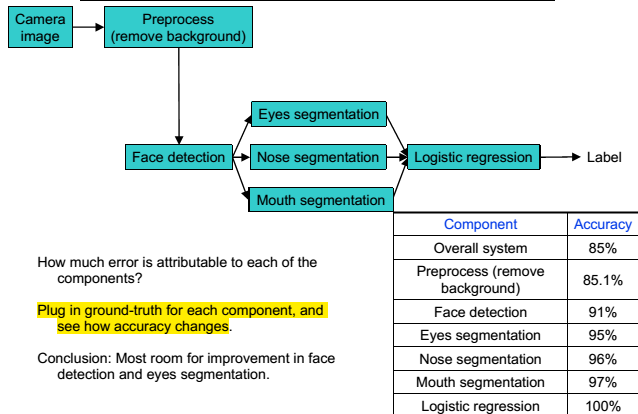 ### 销蚀分析 逐一去除某一成分,分析那一个去除时,准确率下降最快。
### 销蚀分析 逐一去除某一成分,分析那一个去除时,准确率下降最快。 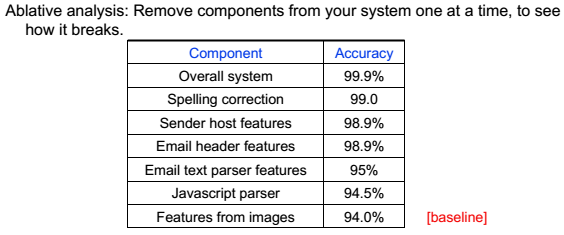


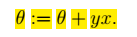


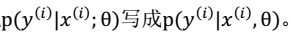 #### 贝叶斯学派(Bayesian) 认为θ是随机变量。 步骤: 1、先验概率p(θ):不同的θ值就有不同的概率。训练集:
#### 贝叶斯学派(Bayesian) 认为θ是随机变量。 步骤: 1、先验概率p(θ):不同的θ值就有不同的概率。训练集: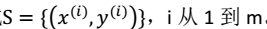 。则:θ的后验概率: >
。则:θ的后验概率: > 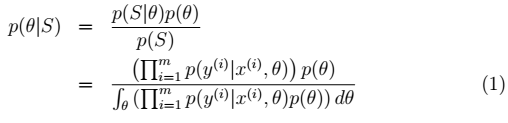 分母有误:
分母有误: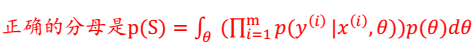
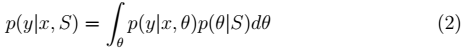 > 注:
> 注: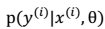 在不同的模型下计算方式不同。比如在贝叶斯 logistic 回归中:
在不同的模型下计算方式不同。比如在贝叶斯 logistic 回归中: 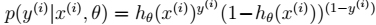 其中,
其中,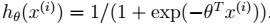
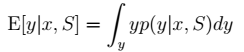
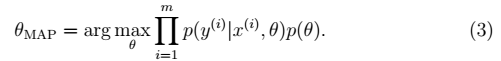
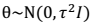 。 3. 贝叶斯最大后验概率估计相对于最大似然估计来说更容易克服过度拟合问题。原因: >> a. 整个公式由两项组成,极大化
。 3. 贝叶斯最大后验概率估计相对于最大似然估计来说更容易克服过度拟合问题。原因: >> a. 整个公式由两项组成,极大化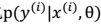 时,不代表此时p(θ)也能最大化。相反,θ是多值高斯分布,极大化时, p(θ)概率反而可能比较小。要达到最大化需要在两者之间达到平衡,也就靠近了偏差和方差线的交叉点。 b. 这个跟机器翻译里的噪声信道模型比较类似,由两个概率决定比有一个概率决定更靠谱。作者声称利用贝叶斯 logistic 回归(使用θMAP的 logistic 回归)应用于文本分类时,即使特征个数 n 远远大于样例个数 m,也很有效。
时,不代表此时p(θ)也能最大化。相反,θ是多值高斯分布,极大化时, p(θ)概率反而可能比较小。要达到最大化需要在两者之间达到平衡,也就靠近了偏差和方差线的交叉点。 b. 这个跟机器翻译里的噪声信道模型比较类似,由两个概率决定比有一个概率决定更靠谱。作者声称利用贝叶斯 logistic 回归(使用θMAP的 logistic 回归)应用于文本分类时,即使特征个数 n 远远大于样例个数 m,也很有效。
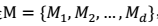 ,那么 SVM、 logistic 回归、神经网络等模型都包含在 M 中。
,那么 SVM、 logistic 回归、神经网络等模型都包含在 M 中。 > - 测试集的比例一般占全部数据的 1/4-1/3。30%是典型值。 > - 由于测试集是和训练集中是两个世界的,因此我们可以认为这里的经验错误接近于泛化错误。 > - 得到的最好模型,在全部数据上重新训练的到所需模型。
> - 测试集的比例一般占全部数据的 1/4-1/3。30%是典型值。 > - 由于测试集是和训练集中是两个世界的,因此我们可以认为这里的经验错误接近于泛化错误。 > - 得到的最好模型,在全部数据上重新训练的到所需模型。 > - 简而言之,这个方法就是将简单交叉验证的测试集改为 1/k,每个模型训练 k 次,测试 k 次,错误率为 k 次的平均。 - 一般讲k 取值为 10 - 数据集非常小的时候:极端情况下,k 可以取值为 m,意味着每次留一个样例做测试,这个称为 leave-one-out cross validation。
> - 简而言之,这个方法就是将简单交叉验证的测试集改为 1/k,每个模型训练 k 次,测试 k 次,错误率为 k 次的平均。 - 一般讲k 取值为 10 - 数据集非常小的时候:极端情况下,k 可以取值为 m,意味着每次留一个样例做测试,这个称为 leave-one-out cross validation。 #### 后向搜索 先将 F 设置为{1,2,..,n},然后每次删除一个特征,并评价,直到达到阈值或者为空,然后选择最佳的 F。 ### 第二种:过滤特征选择(Filter feature selection)
#### 后向搜索 先将 F 设置为{1,2,..,n},然后每次删除一个特征,并评价,直到达到阈值或者为空,然后选择最佳的 F。 ### 第二种:过滤特征选择(Filter feature selection)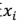 ,i 从 1 到 n,计算
,i 从 1 到 n,计算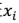 相对于类别标签y的信息量S(i),得到 n 个结果,然后将 n 个S(i)按照从大到小排名,输出前 k 个特征。显然,这样复杂度大大降低,为 O(n)。 > 1、 $x_i
相对于类别标签y的信息量S(i),得到 n 个结果,然后将 n 个S(i)按照从大到小排名,输出前 k 个特征。显然,这样复杂度大大降低,为 O(n)。 > 1、 $x_i 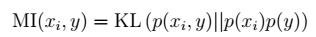 注:
注: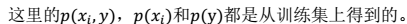

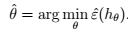 -
- 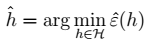 -
- 
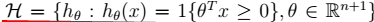
 2、
2、 3、
3、 
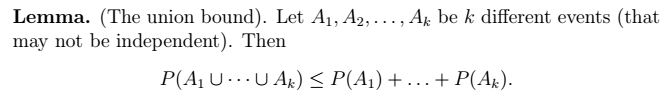 2、Hoeffding不等式
2、Hoeffding不等式 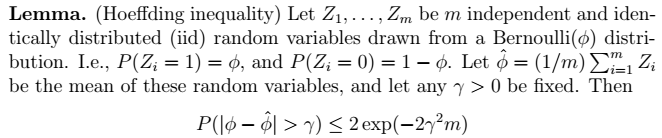 > 利用中心极限定理进行推导。其物理意义如下图所示。其中,
> 利用中心极限定理进行推导。其物理意义如下图所示。其中,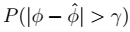 表示阴影的概率,即错误的上届概率。当m增大时,钟形图收缩,误差下降。
表示阴影的概率,即错误的上届概率。当m增大时,钟形图收缩,误差下降。 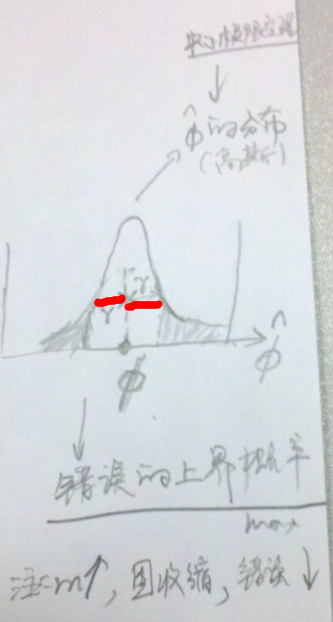
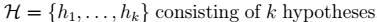 其中,H为:
其中,H为: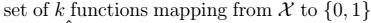 1、
1、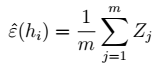 2、
2、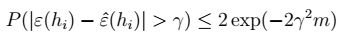 即:
即: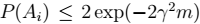 > 表示: -
> 表示: - 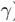 是人为给定的值。
是人为给定的值。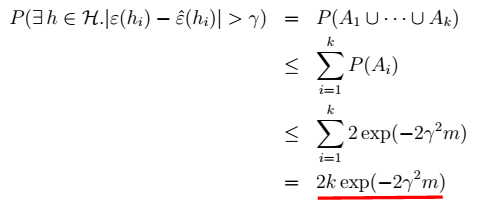 4、对于任意非h:
4、对于任意非h: 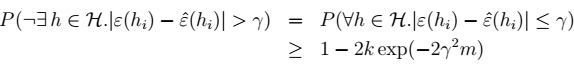 >
> 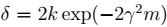 ,当
,当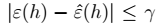 时,我们得到样本的大小:
时,我们得到样本的大小: 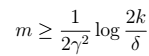 7、进一步,我们得到
7、进一步,我们得到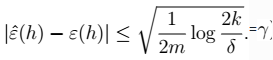 8、对7进行展开:
8、对7进行展开: 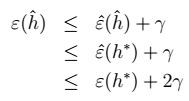 9、最终得到我们的定理:得到
9、最终得到我们的定理:得到 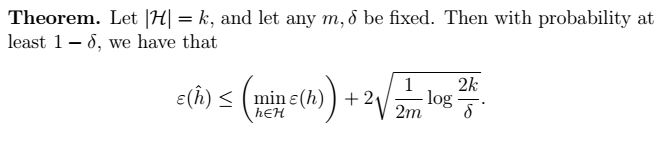 > 物理意义:我们可以近似地认为:
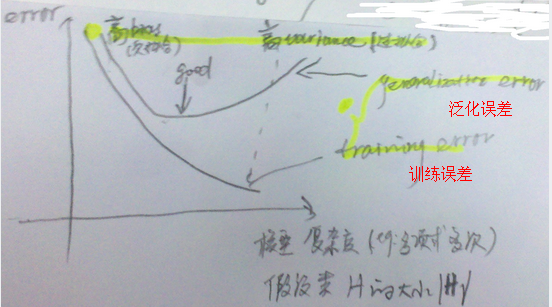
> 物理意义:我们可以近似地认为: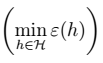 为假设类H的偏差bias;
为假设类H的偏差bias;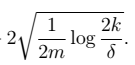 为假设的方差variance。偏差表示误差的大小,随着模型复杂度增大而减小;方差表示拟合得有多好,随着模型复杂度增大,而先减小后增大。如下图:
为假设的方差variance。偏差表示误差的大小,随着模型复杂度增大而减小;方差表示拟合得有多好,随着模型复杂度增大,而先减小后增大。如下图:  ,求m:
,求m: 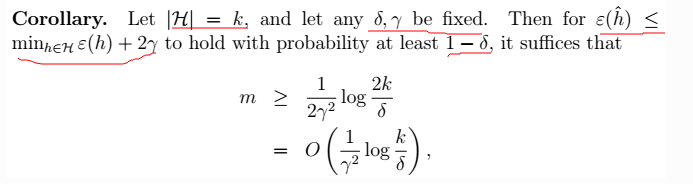 > 两个误差收敛的概率
> 两个误差收敛的概率
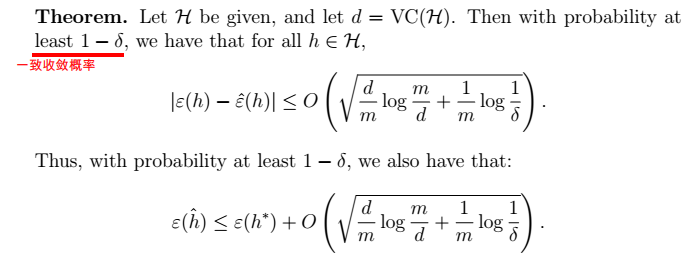 > - m为样本数目; -
> - m为样本数目; - 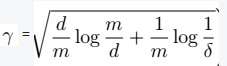 ,从而我们可以得到
,从而我们可以得到