#机器学习15-2--几种算法的对比总结(FA、PCA、混合高斯算法、k-means)
- FA:无监督学习,z连续,服从高斯分布,作为隐含变量;运用EM方法,通过最大化似然函数,对
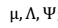 进行参数估计。主要目的:降维。
进行参数估计。主要目的:降维。 - PCA:通过变换矩阵进行降维。
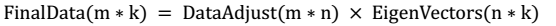
- 混合高斯模型:无监督学习,z离散,服从多项式分布,作为隐含变量;运用EM方法,通过最大化似然函数,对
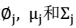 进行参数估计。主要目的:对每个样本进行标签z的分配。
进行参数估计。主要目的:对每个样本进行标签z的分配。 - k-means:无监督学习,通过最小化
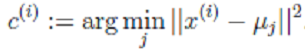 ,使每一类的点到其质心的间隔最小。主要目的:对每个样本进行标签z的分配。
,使每一类的点到其质心的间隔最小。主要目的:对每个样本进行标签z的分配。 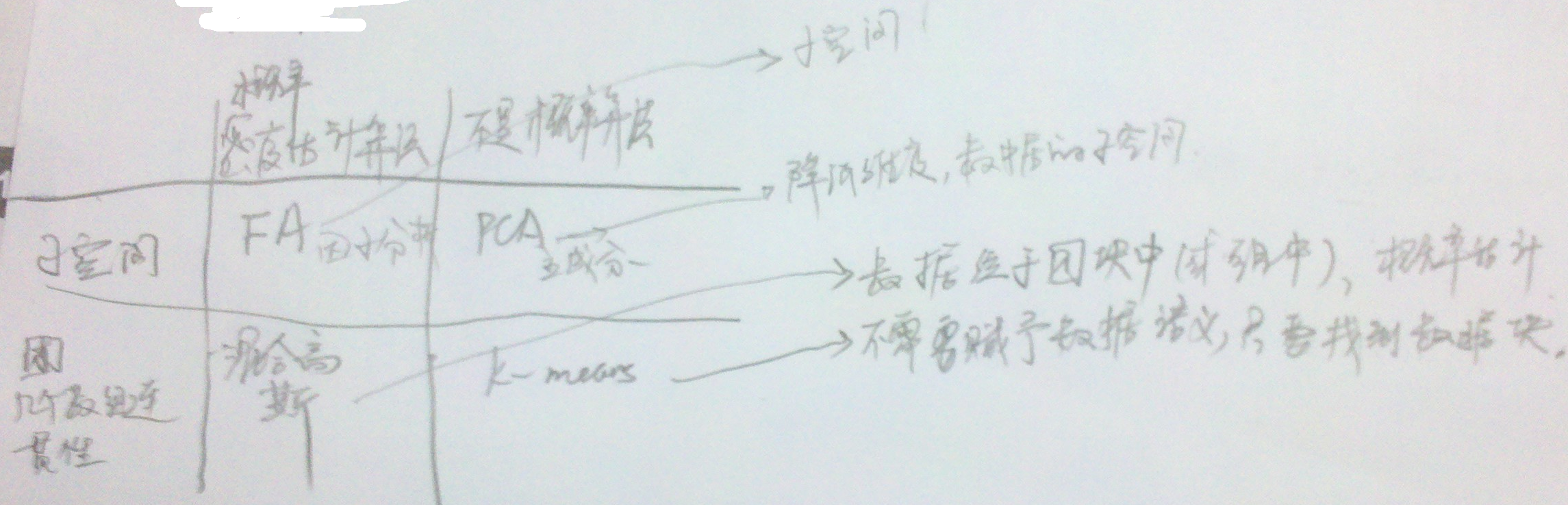
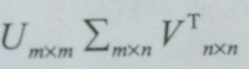 三个参数。
三个参数。 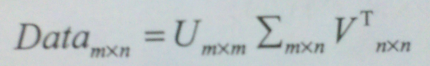 2. 选取合适的k值。
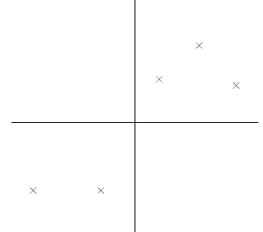
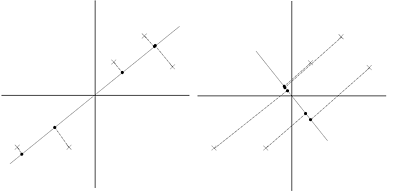
2. 选取合适的k值。 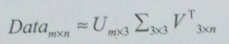 示意图:
示意图:  > 那么,我们的k值是如何获得呢?我们的做法是计算能量信息,保存90%以上的能量即可。能量的计算:所有奇异值求平方和,累加到90%未止。 注:老师上课的推导过程:
> 那么,我们的k值是如何获得呢?我们的做法是计算能量信息,保存90%以上的能量即可。能量的计算:所有奇异值求平方和,累加到90%未止。 注:老师上课的推导过程: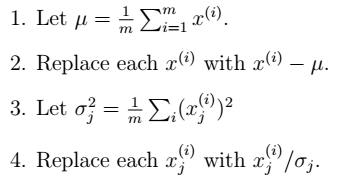 >
> 
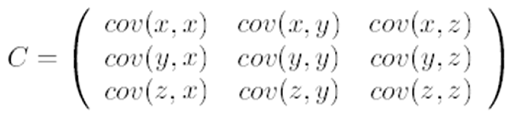
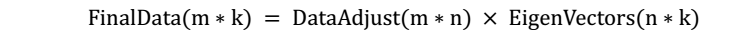
 1. 方差:
1. 方差: 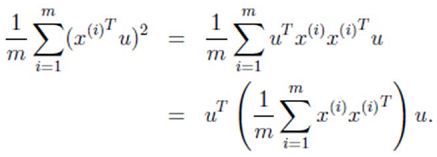
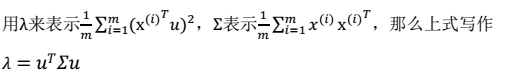 2. 求解最值问题:
2. 求解最值问题: 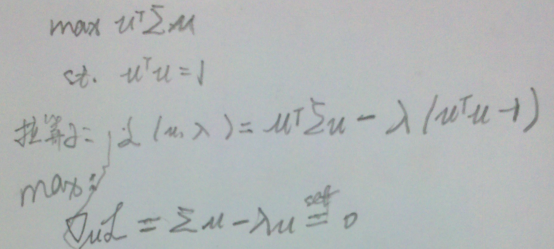 3. 最终解:
3. 最终解: 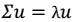 > λ就是Σ的特征值,u是特征向量。最佳的投影直线是特征值λ最大时对应的特征向量,其次是λ第二大对应的特征向量,依次类推。
> λ就是Σ的特征值,u是特征向量。最佳的投影直线是特征值λ最大时对应的特征向量,其次是λ第二大对应的特征向量,依次类推。 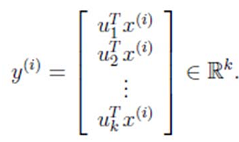 其中的第j 维就是
其中的第j 维就是 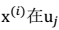 上的投影。 通过选取最大的k个u,使得方差较小的特征(如噪声)被丢弃。
上的投影。 通过选取最大的k个u,使得方差较小的特征(如噪声)被丢弃。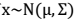
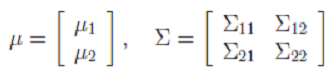 2. 边缘分布
2. 边缘分布 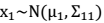 3. 条件概率分布
3. 条件概率分布 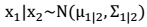
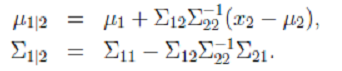
 > eg:从1维到2维: 1维:
> eg:从1维到2维: 1维:  2维
2维 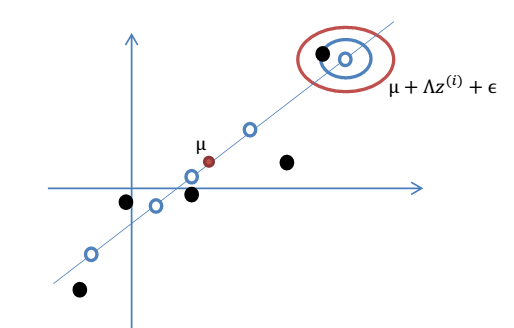 2. 我们令:
2. 我们令: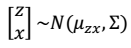 3. 下面经过推导,求得
3. 下面经过推导,求得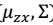 的具体值:
的具体值: 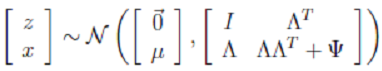 4. 因此,我们得到x的边缘分布:
4. 因此,我们得到x的边缘分布: 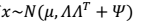 5. 从而我们对样本
5. 从而我们对样本 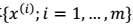 进行最大似然估计:
进行最大似然估计: 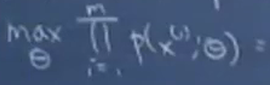
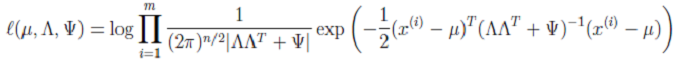 > 但是,当似然函数最大时,我们得不到解析解(比如,一元二次方程的通解形式)。根据之前对参数估计的理解,在有隐含变量 z 时,我们可以考虑使用 EM 来进行估计。
> 但是,当似然函数最大时,我们得不到解析解(比如,一元二次方程的通解形式)。根据之前对参数估计的理解,在有隐含变量 z 时,我们可以考虑使用 EM 来进行估计。 > 注:这里的
> 注:这里的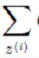 要改写为积分符号
要改写为积分符号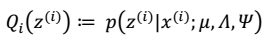 根据前面的结论有:
根据前面的结论有: 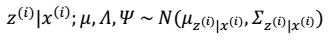
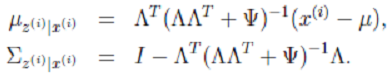 2. 根据多元高斯公式得:
2. 根据多元高斯公式得: 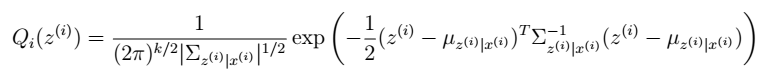
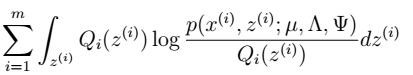
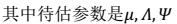 4. 通过参数估计,我们最终可以得到:
4. 通过参数估计,我们最终可以得到: 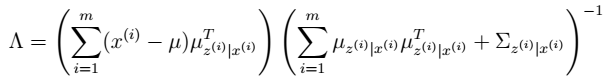
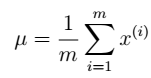
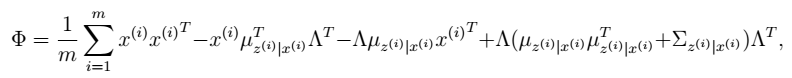 然后将Φ上的对角线上元素抽取出来放到对应的Ψ中,就得到了Ψ。
然后将Φ上的对角线上元素抽取出来放到对应的Ψ中,就得到了Ψ。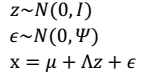 2. 因子分析(factor analysis)是一种数据简化的技术。原始的变量是可观测的显在变量,而假想变量是不可观测的潜在变量,称为因子。 3. 因子分析与回归分析不同,因子分析中的因子是一个比较抽象的概念,而回归因子有非常明确的实际意义 4. 主成分分析分析与因子分析也有不同,主成分分析仅仅是变量变换,而因子分析需要构造因子模型。 > 主成分分析:原始变量的线性组合表示新的综合变量,即主成分; 因子分析:潜在的假想变量和随机影响变量的线性组合表示原始变量。
2. 因子分析(factor analysis)是一种数据简化的技术。原始的变量是可观测的显在变量,而假想变量是不可观测的潜在变量,称为因子。 3. 因子分析与回归分析不同,因子分析中的因子是一个比较抽象的概念,而回归因子有非常明确的实际意义 4. 主成分分析分析与因子分析也有不同,主成分分析仅仅是变量变换,而因子分析需要构造因子模型。 > 主成分分析:原始变量的线性组合表示新的综合变量,即主成分; 因子分析:潜在的假想变量和随机影响变量的线性组合表示原始变量。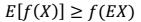 > - 凸函数:
> - 凸函数: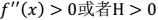 - 如果 f 是严格凸函数,那
- 如果 f 是严格凸函数,那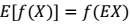 当且仅当
当且仅当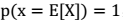 。即:也就是说 X 是常量(后面会用到这个结论)。𞀊- Jensen 不等式应用于凹函数时,不等号方向反向,也就是
。即:也就是说 X 是常量(后面会用到这个结论)。𞀊- Jensen 不等式应用于凹函数时,不等号方向反向,也就是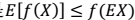 。后面的log函数就是凹函数。
。后面的log函数就是凹函数。
 所以可见用EM算法的模型(高斯混合模型,朴素贝叶斯模型)都是求p(x,y)联合概率,为生成模型。
所以可见用EM算法的模型(高斯混合模型,朴素贝叶斯模型)都是求p(x,y)联合概率,为生成模型。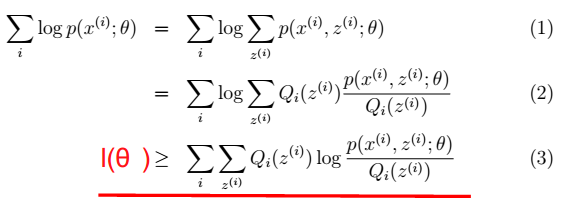 > 其中,
> 其中,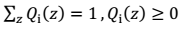 如果 z 是连续性的,那么
如果 z 是连续性的,那么 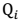 是概率密度函数,需要将求和符号换做积分符号(因子分析模型是如此),即:
是概率密度函数,需要将求和符号换做积分符号(因子分析模型是如此),即: 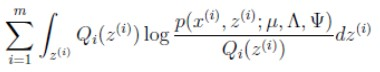
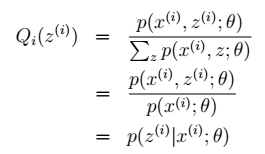 > -
> - 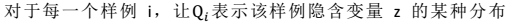 > - z只受参数θ影响:
> - z只受参数θ影响: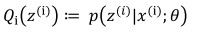
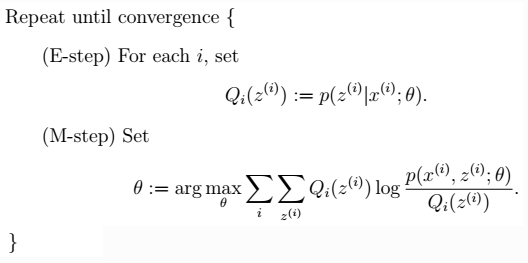 > - 注:在m步中,最终是对参数θ进行估计,而这一步具体到高斯混合模型,则θ有三个参数:
> - 注:在m步中,最终是对参数θ进行估计,而这一步具体到高斯混合模型,则θ有三个参数: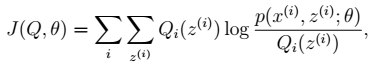 从前面的推导中我们知道ℓ(θ) ≥ J(Q, θ),EM 可以看作是 J 的坐标上升法,E 步固定θ,优化Q;M 步固定Q优化θ。
从前面的推导中我们知道ℓ(θ) ≥ J(Q, θ),EM 可以看作是 J 的坐标上升法,E 步固定θ,优化Q;M 步固定Q优化θ。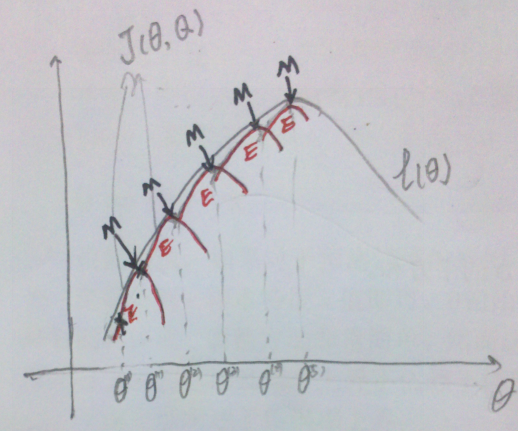 > 其中,红色线表示每一步的J(Q, θ)。E步:确定红线部分。M步:确定当前红线部分J(Q, θ)的极值点。最终得到局部最优解。
> 其中,红色线表示每一步的J(Q, θ)。E步:确定红线部分。M步:确定当前红线部分J(Q, θ)的极值点。最终得到局部最优解。
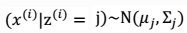 。由此可以得到联合分布:
。由此可以得到联合分布: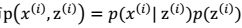 。
。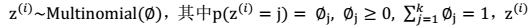 有 k 个值{1,…,k} 可以选取。
有 k 个值{1,…,k} 可以选取。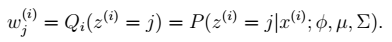 M步 2、我们需要在固定
M步 2、我们需要在固定 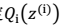 后最大化最大似然估计,求解
后最大化最大似然估计,求解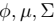
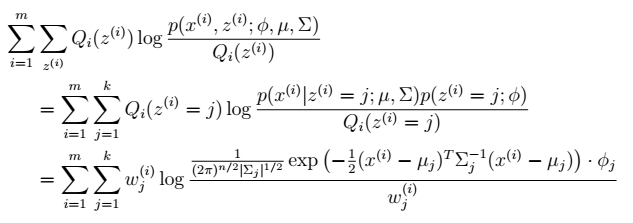 >
> 
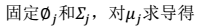
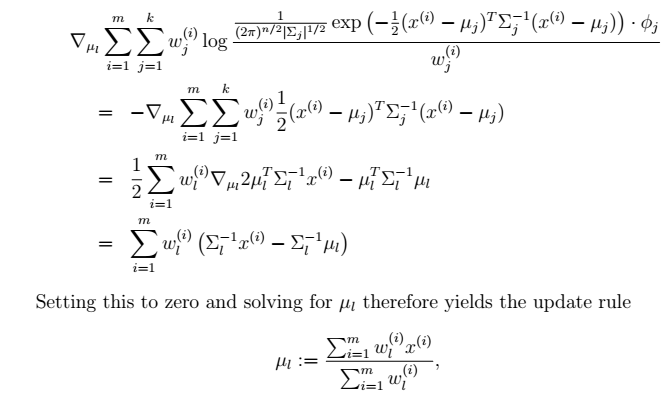 2.
2. 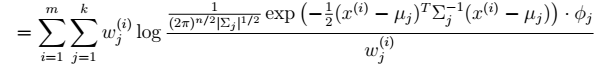 在∅和μ确定后,分子上面的一串都是常数了,实际上需要优化的公式是:
在∅和μ确定后,分子上面的一串都是常数了,实际上需要优化的公式是: 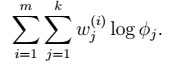
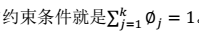 显然这是一个,有约束条件的规划问题。我们采用前面的拉格朗日方法:
显然这是一个,有约束条件的规划问题。我们采用前面的拉格朗日方法:  3. Σ的推导也类似,不过稍微复杂一些,毕竟是矩阵。
3. Σ的推导也类似,不过稍微复杂一些,毕竟是矩阵。 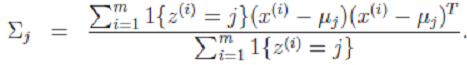

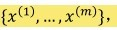 , 每个文本
, 每个文本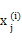 = { wordj 是否出现在文本i 里} 我们要对
= { wordj 是否出现在文本i 里} 我们要对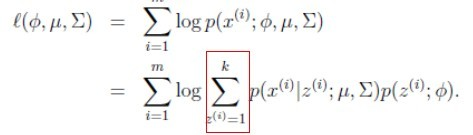 2、由贝叶斯公式可知:
2、由贝叶斯公式可知: 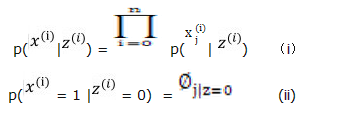 3、E步:
3、E步: 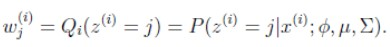 > 注:这里三个参数phi,mu,sigma,改成,
> 注:这里三个参数phi,mu,sigma,改成,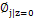 ,
,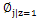 与
与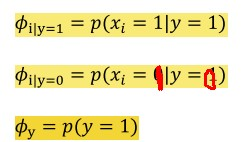 得到:
得到: 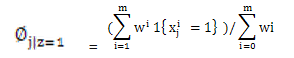 > 这里Wi表示文本来自于类1,分子Σ表示:类1且包含词j的文档个数,分布表示类1的文档总数。所以全式表示:类1包含词j的比率。 EM算法不能做出绝对的假设0或者1,所以只能用Wi表示,最终Wi的值会靠近0或1,在数值上与0或1无分别。
> 这里Wi表示文本来自于类1,分子Σ表示:类1且包含词j的文档个数,分布表示类1的文档总数。所以全式表示:类1包含词j的比率。 EM算法不能做出绝对的假设0或者1,所以只能用Wi表示,最终Wi的值会靠近0或1,在数值上与0或1无分别。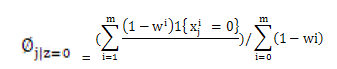 > 全式表示:类0包含词j的比率
> 全式表示:类0包含词j的比率