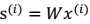Apache Ambari
用来创建、管理、监视 Hadoop 的集群,但是这里的 Hadoop 是广义,指的是 Hadoop 整个生态圈(例如 Hive,Hbase,Sqoop,Zookeeper 等),而并不仅是特指 Hadoop。用一句话来说,Ambari 就是为了让 Hadoop 以及相关的大数据软件更容易使用的一个工具。
Ambari 自身也是一个分布式架构的软件,主要由两部分组成:Ambari Server 和 Ambari Agent。简单来说,用户通过 Ambari Server 通知 Ambari Agent 安装对应的软件;Agent 会定时地发送各个机器每个软件模块的状态给 Ambari Server,最终这些状态信息会呈现在 Ambari 的 GUI,方便用户了解到集群的各种状态,并进行相应的维护。
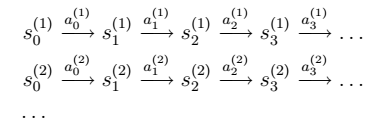 我们定义Model或者Simulator为:
我们定义Model或者Simulator为: 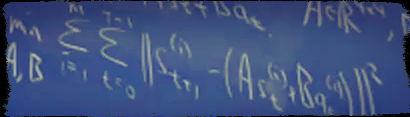
 > 大致思路:公有m个状态。通过随机采样k个状态s,求平均值获得
> 大致思路:公有m个状态。通过随机采样k个状态s,求平均值获得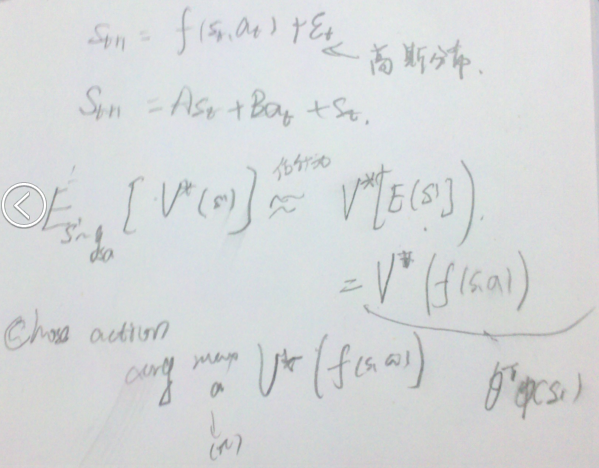 > 其中,${}_{t} $为误差,服从高斯分布。
> 其中,${}_{t} $为误差,服从高斯分布。



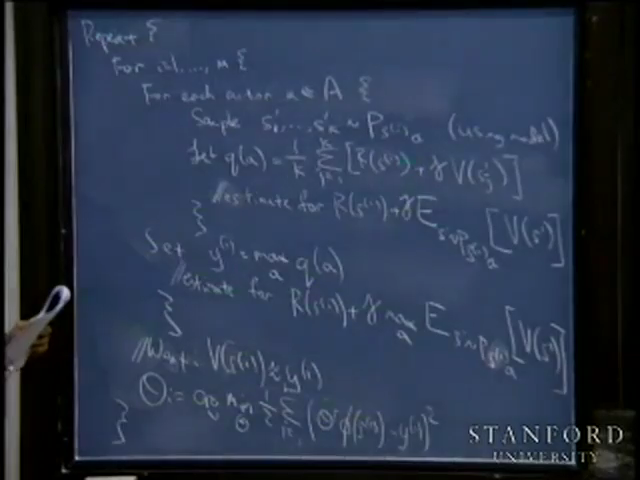

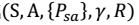
 2. 概念: - 值函数: 为了区分不同π的好坏,并定义在当前状态下,执行某个策略π后,出现的结果的好坏, 需要定义值函数:
2. 概念: - 值函数: 为了区分不同π的好坏,并定义在当前状态下,执行某个策略π后,出现的结果的好坏, 需要定义值函数: 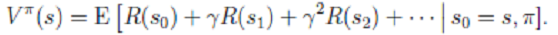 - 策略(pllicy):
- 策略(pllicy):  ###公式推导(最优值函数和最优策略) 3. 对于如下问题,Robot开始位于(3,1)位置。目的是右上角。可能有11个状态。
###公式推导(最优值函数和最优策略) 3. 对于如下问题,Robot开始位于(3,1)位置。目的是右上角。可能有11个状态。 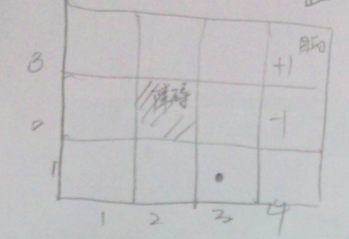 > - 行走的概率:
> - 行走的概率:  > - 回报函数
> - 回报函数 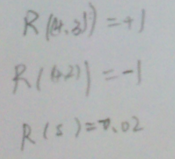 > - 在某一点时的值函数。对于上述问题,有11个方程,11个未知量。
> - 在某一点时的值函数。对于上述问题,有11个方程,11个未知量。  4. 进一步化简,我们得到
4. 进一步化简,我们得到 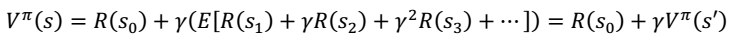 Bellman 等式
Bellman 等式 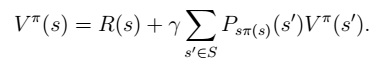 其中,
其中,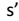 表示下一个状态。 5. 定义最优值函数:
表示下一个状态。 5. 定义最优值函数: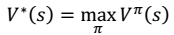 6. 最终,我们得到想要的最优值函数和最优策略:
6. 最终,我们得到想要的最优值函数和最优策略: 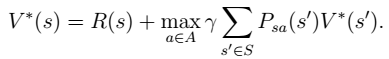
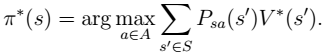 7. 这里需要注意的是,如果我们能够求得每个 s 下最优的 a,那么从全局来看,
7. 这里需要注意的是,如果我们能够求得每个 s 下最优的 a,那么从全局来看,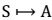 的 映射即可生成,而生成的这个映射是最优映射,称为
的 映射即可生成,而生成的这个映射是最优映射,称为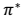 。
。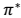 针对全局的 s,确定了每一个 s的下一个行动 a,不会因为初始状态 s 选取的不同而不同。
针对全局的 s,确定了每一个 s的下一个行动 a,不会因为初始状态 s 选取的不同而不同。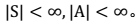 ### 值迭代法 1. 过程
### 值迭代法 1. 过程 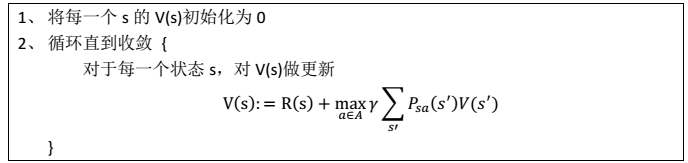 其中,迭代公式也可以写作:
其中,迭代公式也可以写作: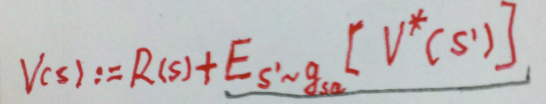 2. 内循环的有两种策略:
2. 内循环的有两种策略:  3. 两种迭代法最终收敛到
3. 两种迭代法最终收敛到
 > 注:在1-(a)中,我们认为得到的V为最优值函数。然后,在(b)中,进行更新得到最优策略。一直重复,知道得到真正的最优策略
> 注:在1-(a)中,我们认为得到的V为最优值函数。然后,在(b)中,进行更新得到最优策略。一直重复,知道得到真正的最优策略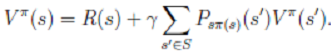 (b)步实际上就是根据(a)步的结果挑选出当前状态 s 下,最优的 a,然后对π(s)做更新。 > 这里的两个步骤,相当于求解11(状态个数)个线性方程。如果状态非常多,显然计算量相当大。
(b)步实际上就是根据(a)步的结果挑选出当前状态 s 下,最优的 a,然后对π(s)做更新。 > 这里的两个步骤,相当于求解11(状态个数)个线性方程。如果状态非常多,显然计算量相当大。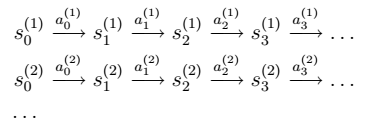 > 其中:
> 其中: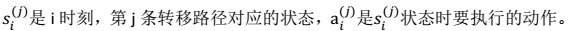 2. 如果我们获得了很多上面类似的转移链(相当于有了样本),那么我们就可以使用最大似然估计来估计状态转移概率。
2. 如果我们获得了很多上面类似的转移链(相当于有了样本),那么我们就可以使用最大似然估计来估计状态转移概率。 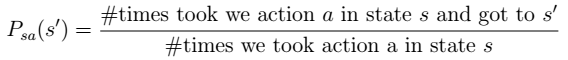 > 注:分子是从 s 状态执行动作 a 后到达 s’的次数,分母是在状态 s 时,执行 a 的次数。两者相除就是在 s 状态下执行 a 后,会转移到 s’的概率。 3. 同样,如果回报函数未知,那么我们认为 R(s)为在 s 状态下已经观测到的回报均值。 4. 我们将参数估计和值迭代结合起来(在不知道状态转移概率情况下)的流程如下:
> 注:分子是从 s 状态执行动作 a 后到达 s’的次数,分母是在状态 s 时,执行 a 的次数。两者相除就是在 s 状态下执行 a 后,会转移到 s’的概率。 3. 同样,如果回报函数未知,那么我们认为 R(s)为在 s 状态下已经观测到的回报均值。 4. 我们将参数估计和值迭代结合起来(在不知道状态转移概率情况下)的流程如下:  > 在(b)步中我们要做值更新,也是一个循环迭代的过程,在上节中,我们通过将 V 初始化为 0,然后进行迭代来求解 V。嵌套到上面的过程后,如果每次初始化 V 为 0,然后迭代更新, 就会很慢。一个加快速度的方法是每次将 V 初始化为上一次大循环中得到的 V。 也就是说 V 的初值衔接了上次的结果。
> 在(b)步中我们要做值更新,也是一个循环迭代的过程,在上节中,我们通过将 V 初始化为 0,然后进行迭代来求解 V。嵌套到上面的过程后,如果每次初始化 V 为 0,然后迭代更新, 就会很慢。一个加快速度的方法是每次将 V 初始化为上一次大循环中得到的 V。 也就是说 V 的初值衔接了上次的结果。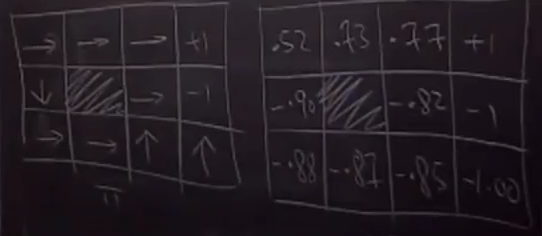

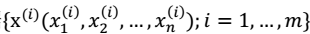 。其中:i 表示采样的时间顺序,也就是说共得到了 m 组采样,每一组采样都是 n 维的。 - 我们的目标是单单从这 m 组采样数据中分辨出每个人说话的信号s。有 n 个信号源
。其中:i 表示采样的时间顺序,也就是说共得到了 m 组采样,每一组采样都是 n 维的。 - 我们的目标是单单从这 m 组采样数据中分辨出每个人说话的信号s。有 n 个信号源 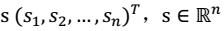 ,s相互独立。 - A 是一个未知的混合矩阵(mixing matrix),用来组合叠加信号 s。 1. 我们可以得到:
,s相互独立。 - A 是一个未知的混合矩阵(mixing matrix),用来组合叠加信号 s。 1. 我们可以得到: 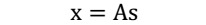 > 其中, x 不是一个向量,是一个矩阵 2. 其中每个列向量
> 其中, x 不是一个向量,是一个矩阵 2. 其中每个列向量 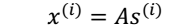
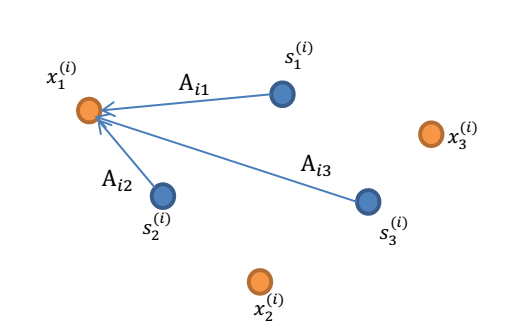 3. A 和 s 都是未知的,x 是已知的,我们要想办法根据 x 来推出 s。这个过程也称作为盲信号分离。
3. A 和 s 都是未知的,x 是已知的,我们要想办法根据 x 来推出 s。这个过程也称作为盲信号分离。 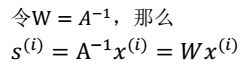
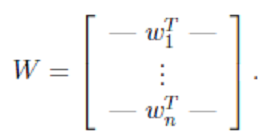 4. 最终得到:
4. 最终得到: 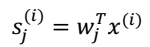 > -
> - 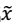 (其协方差矩阵是
(其协方差矩阵是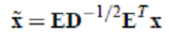 > - 其中,
> - 其中, 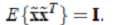 > - 其中使用特征值分解来得到 E(特征向量矩阵)和 D(特征值对角矩阵) ,计算公式为
> - 其中使用特征值分解来得到 E(特征向量矩阵)和 D(特征值对角矩阵) ,计算公式为 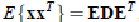
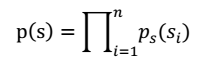 > 注:每个人发出的声音信号s各自独立。
> 注:每个人发出的声音信号s各自独立。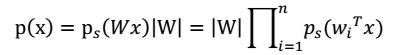
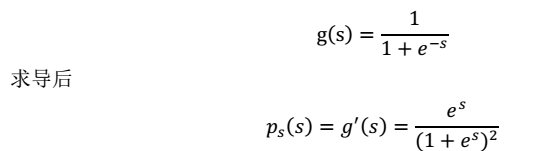 这就是 s 的密度函数。这里 s 是实数。
这就是 s 的密度函数。这里 s 是实数。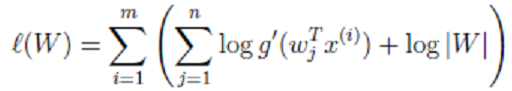 >
>  最终,我们求得:
最终,我们求得: 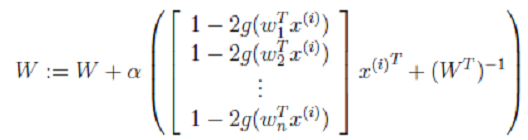 >> 其中α是梯度上升速率,人为指定。
>> 其中α是梯度上升速率,人为指定。