抽时间将数据驱动的一些内容进行了总结,先整理下面五篇,后续将不断完善。。
1. 概述
大型集群系统中,可能存在软件问题和硬件问题导致的系统故障,严重影响了系统的高可用性。这就要求7*24小时,对系统不间断监控。这就意味着需要不间断地监控大量时间序列数据,以便检测系统潜在的故障和异常现象。然而,实际当中的系统异常很多,且不容易发现;从而导致人工方式监控方式效率很低。
异常场景本质上是一个或者多个数据点;数据点一般在系统运行过程中产生,且能反应系统的功能是否正常,多以日志形式呈现。当系统功能发生异常时,就会产生异常数据。快速高效地发现这些异常值,对于快速止损具有重要意义。对此,我们提出一种基于时间序列的异常识别模型,用来及时发现异常。
对于多数系统,一般都有成功率、流量等指标,故障发生时,这些指标也会出现响应的异常。我们将系统成功率、流量统一称为特征值变量,并对其进行建模,从而方便后续其它特征变量的扩展。为了更好地感知这些特征变量的突变,需要对特征变量进行计算处理或者空间转换。那么异常识别问题就转换为以下两个问题:
- 特征变量的计算处理和转换
- 突变的判断
针对这两个关键问题,我们将在下文中进行建模和分析。
2. 异常识别
如下图,通过计算器进行特征变量的计算处理和转换,通过异常检测器来判断数值的突变,从而解决上面的两个问题。其中,异常检测器由比较器和决策器组成。
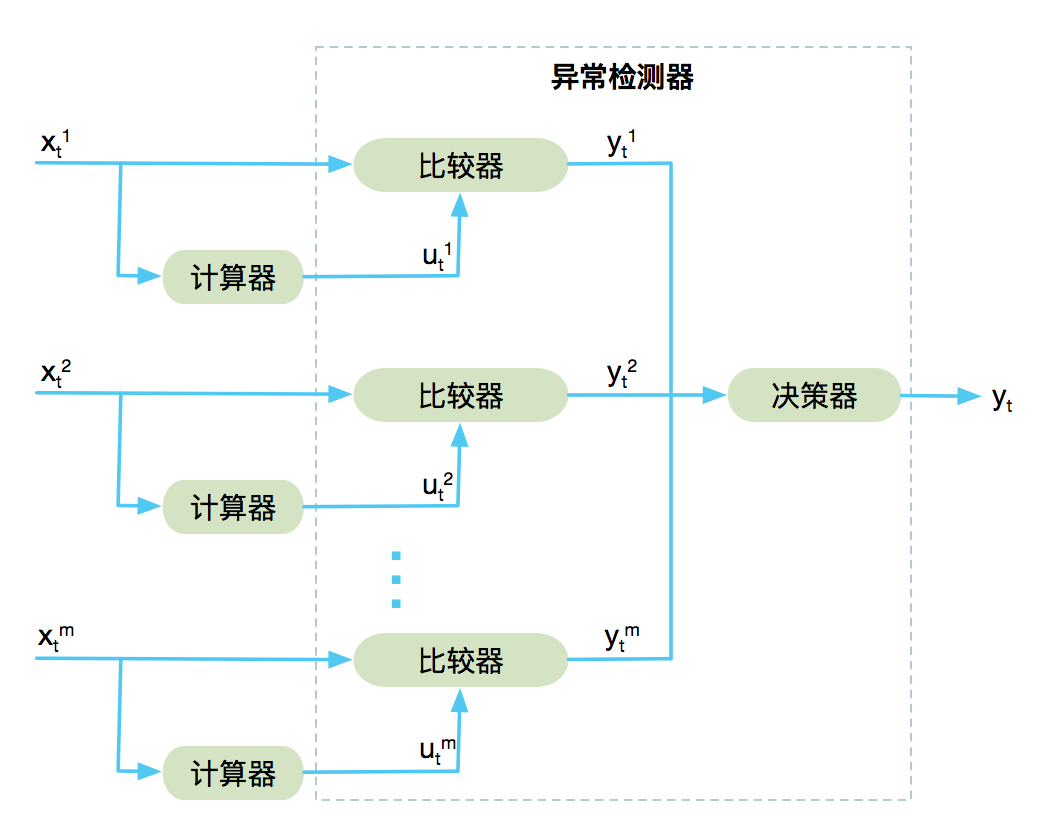
对于给定时间序列二维矩阵\(X=\{x^m_t∈R:∀t≥0, ∀m≥0\}\) ,\(x_t^m\)为\(t\)时刻的第m个指标的真实数据,\(u_t^m\)表示时间\(t\)的\(x_t^m\)的计算值,\(y_t^m\)为第m个指标的输出结果,\(y_t\)为整体预测结果。
\(x_t^m\)通过计算器得到计算值\(u_t^m\),然后\(x_t^m\) 和 \(u_t^m\)分别作为比较器的输入,得到第m个指标的输出\(y_t^m\)。\(y_t^1\),\(y_t^2\)…\(y_t^m\)作为决策器的输入得到\(y_t\)。\(y_t\)是一个二元值,可以用TRUE(表示输出数据正常),FALSE(表示输入数据异常)表示。下面对计算器和检测器进行说明。
2.1 计算器
计算器用来对输入值\(x_t^m\) 进行计算或者空间转换,从而得到特征变量的计算值\(u_t^m\)。一般情况下,特征变量具有趋势性、周期性等特征。基于这些特征,计算值的获取,可以使用以下三种方式:累计窗口均值计算器、基于趋势性的环比计算器、基于周期性的同比计算器。
2.1.1 累积窗口均值计算器
输入值为\(x_t\)(为了方便省略指标参数m),如果直接只用单个点\(x_t\)的抖动来判断,受噪声影响较大。因此,使用累积窗口均值的方式:
\[ u(t)={\dfrac{x_t+x_{t-1}+...+x_{t-w+1}}{w}} \tag{1}\]
其中,\(w\)为累计窗口的大小。通过窗口平滑之后,会过滤掉尖刺等噪声。
2.1.2 基于趋势性的计算器
为了描述数据的趋势性,引入环比类算法。对\(x_t\)进行空间转换,得到环比,再使用检测器进行检测。
\[u(t)={\dfrac{x_t+x_{t-1}+...+x_{t-w+1}}{x_{t-w}+x_{t-w-1}+...+x_{t-2w+1}}} \tag{2}\]
其中,分子为当前窗口\(w\)内的数据,分母为上一窗口\(w\)内数据。通过窗口\(w\)对数据进行平滑。
2.1.3 基于周期性的计算器
为了描述数据的周期性,引入同比算法。当同比值过大或者过小时,认为发生故障。同比公式如下:
\[u(t)={\dfrac{x_t+x_{t-1}+...+x_{t-w+1}}{x_{t-kT}+x_{t-kT-1}+...+x_{t-kT-w+1}}} \tag{3} \]
其中\(T\)为周期,\(k\)表示第几个周期。一般选取\(k\)为1、7、30,来表示昨天、上周、上个月。
2.1.4 其他类型计算器
计算器还可以使用其他算法,包括:
- 统计类算法:包括同比、环比算法的改进,或者其他统计算法。此时,计算器的输出结果为预测值,预测值和输入值进行比较即可。
- 时序型算法:包含ARIMA、Holter-Winter等时序型算法。计算器的输出结果为预测值。
- 机器学习:根据有监督、无监督、深度学习(LSTM)等算法,训练出的模型即为计算器。此时,计算器的输出结果一般为归一化的值,根据归一化的值进行比较。
这些算法,在这里不再做深入研究和阐述。
2.2 异常检测器
当数据出现异常时,计算值会出现较大偏差,该偏差由异常检测器来判断。异常检测器由比较器和决策器组成,计算值和真实值通过该模块后,得到最终预测结果。
2.2.1 比较器
比较器的本质是求解如下公式的过程:
\[f(x^m_t,u^m_t;h^m)\ \ = \ \ boolean \tag{4}\]
其中,\(x^m_t\)为真实值,\(u\)为计算值,\(h^m\)为阈值参数,\(boolean\)为结果TRUE/FALSE。真实值已知,计算值通过计算器得到;剩下的阈值参数\(h^m\),则需要根据故障发生时的实际值进行参数估计。
很多场景下,该公式还可以简化为:\(f(u^m_t;h^m)\ \ = \ \ boolean\) ,即计算值直接和阈值比较即可。
2.2.1.1 比较器种类
比较器有两种:相对值比较器和绝对值比较器。给定计算值\(u^m_t\)和输入值\(x^m_t\),得到绝对值比较器:
\[f= x_t^m−u_t^m\ \ opretor \ \ h^m \tag{5}\]
其中,\(opretor\)为比较操作符,比如> < >= <=。由于\(u_t\)由\(x_t\)得到,所以很多情况下公式可以简化为 $ u_t^m opretor h_t^m$,即确定计算值的阈值即可。
对于一些场景来说,需要捕获特征变量的相对性。因此,引入相对值比较器:
\[ f={\dfrac{x_t^m−u_t^m}{u_t^m}}\ \ opretor \ \ h^m \tag{6} \]
通过对相对值比较器进行阈值处理,既可以检测异常值,同时还能对期望值进行归一化。
2.2.1.2 比较器阈值\(h\)的选取
一般情况下,阈值参数决定了异常检测模块的敏感度。最优阈值的选择,取决于数据分布的性质以及先验数据。一般情况下,阈值的选取方法为:
- 方法一:跟踪一组故障数据和正常数据,根据经验估计阈值。
- 方法二:跟踪一组故障数据和正常数据,根据经验,并结合
3σ准则确定,来确定阈值。(特征变量或者特征变量的组合,服从正态分布)
2.2.2 决策器
如下公式,基于逻辑操作符,对比较器结果进行合并.
- 方式一:逻辑组合
\[ y_t=y_t^1 \ \ \&| \ \ y_t^2 \ \ \&| \ \ y_t^3 \ \ \&| \ \ ... \ \ y_t^m \tag{7}\]
其中,\(|\)表示逻辑或操作,\(\&\)表示逻辑与操作。
方式二:权重设置法
\[y_t=k_1*y_t^1 \ \ + \ \ k_2*y_t^2 \ \ + \ \ k_3*y_t^3 \ \ + \ \ ... \ \ k_m* y_t^m \tag{8}\]
其中,\(k_m\)为系数,这种方式一般适合基本无负样本的场景,参数的确定需要使用层次分析法,将在后面的文章进行说明。
3. 故障止损
上面主要阐述了异常识别的方式。如果条件过于严格,刚开始并不容易被识别出来;如果条件过松,可能导致误识别。对此,我们将止损策略分为两级:
- 级别一:预警。对于不能完全确定故障发生的场景,使用级别一。
- 级别二:预警+止损(踢IDC)。对于能确定IDC故障的场景,使用级别二。
4. 实际场景应用
下面通过一个规则的场景,进行举例说明。假如存在如下异常场景:
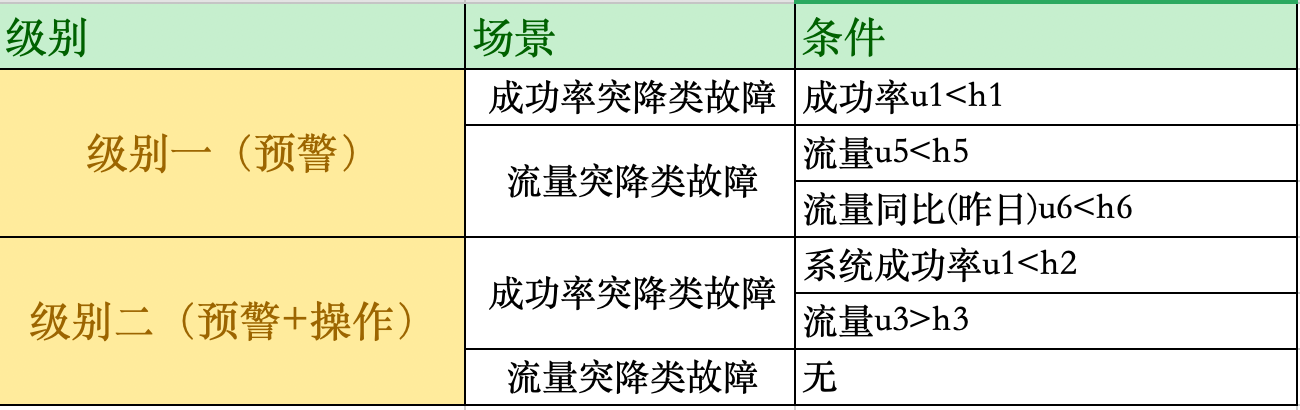
体现在模型中,则级别一(预警)的模型图
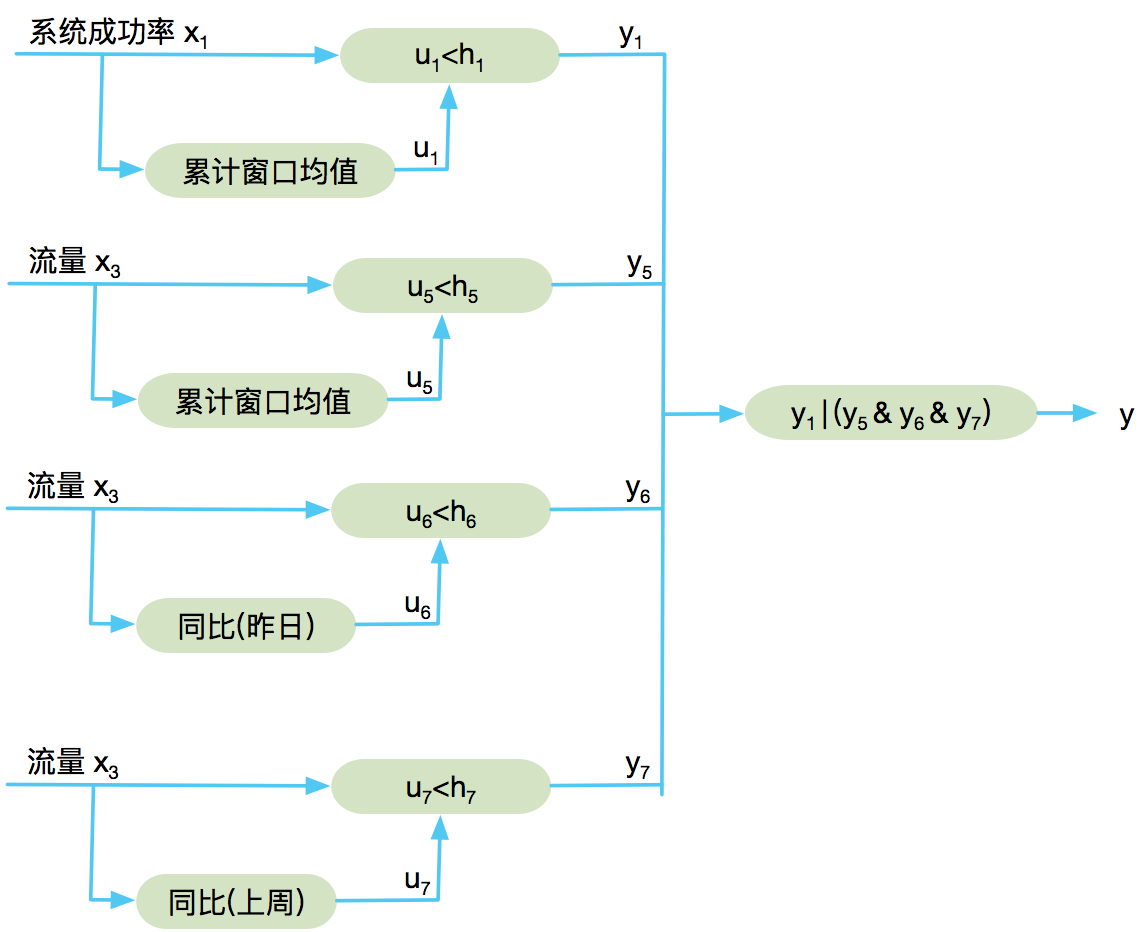
级别二(预警+踢IDC)的模型图:
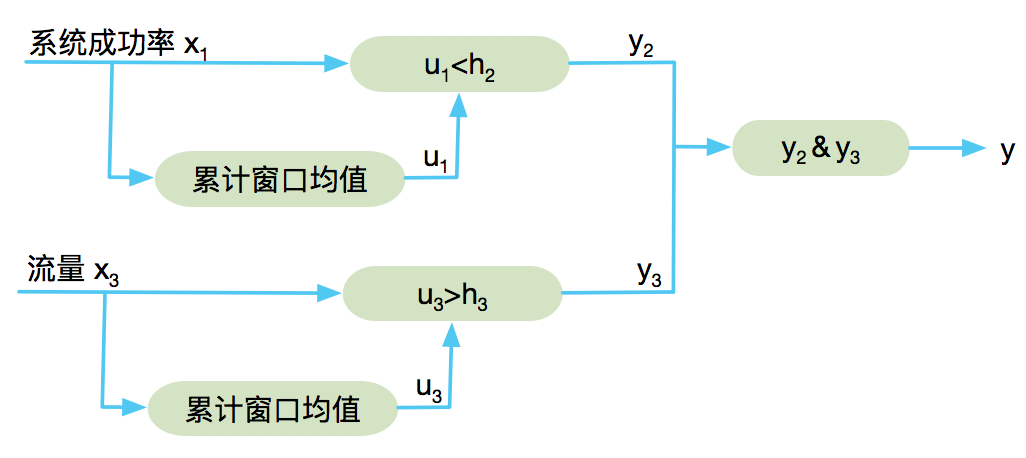
最终,得到故障识别规则:
- 级别一触发条件: \(u_1<h_1 \ \ | \ \ (u5<h5 \ \ \& \ \ u6<h6 \ \ \& \ \ u7<h7 )\)
- 级别二触发条件:\(u_1<h_2 \ \ \& \ \ u_3>h_3\)
其中,\(h_1, h_2,h_3,h_5,h_6,h_7\)为阈值参数。需要结合经验和实际数据估计得到。
5. 小结
本文主要基于时间序列的数据,提出了异常场景识别模型,并重点对基于规则的识别进行了说明。

